
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет доверительных интервалов
Доверительные интервалы дают больше информации о параметре, чем точечная оценка, так как показывают совокупность допустимых значений.
Понятие доверительного интервала тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям
Например, если класс точности прибора 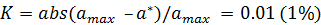 а этот прибор – манометр с максимальным значением давления по шкале 100кгс/см2, то абсолютная погрешность этого прибора
а этот прибор – манометр с максимальным значением давления по шкале 100кгс/см2, то абсолютная погрешность этого прибора
 ,
,
следовательно,  =0,5 ат .
=0,5 ат .
Пусть имеется выборка объемом  значений случайной величины. Оценкой
значений случайной величины. Оценкой  является среднее выборки:
является среднее выборки: 
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально, доказано, что 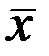 также имеет нормальное распределение с математическим ожиданием
также имеет нормальное распределение с математическим ожиданием  и среднеквадратическим отклонением (стандартной ошибкой)
и среднеквадратическим отклонением (стандартной ошибкой) 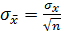 .Тогда
.Тогда
 (4.3)
(4.3)
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 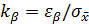 . Тогда доверительный интервал для математического ожидания будет иметь вид
. Тогда доверительный интервал для математического ожидания будет иметь вид
 или
или
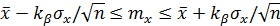
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1) приближенный – при  более 50 заменяют неизвестные параметры их оценками;
более 50 заменяют неизвестные параметры их оценками;
2) от случайной величины  переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра
переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра  , а зависит только от объема выборки
, а зависит только от объема выборки  и от вида распределения величины
и от вида распределения величины  . Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили

Если выразить через  ,
,

На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 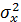 неизвестна, поэтому для построения доверительного интервала математического ожидания используют выборочную дисперсию
неизвестна, поэтому для построения доверительного интервала математического ожидания используют выборочную дисперсию  и приведенную случайную величину:
и приведенную случайную величину:

 – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(
– случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы( 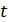 – распределение или распределение Стьюдента). При больших значениях
– распределение или распределение Стьюдента). При больших значениях  распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала
распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала

Дата добавления: 2014-11-13; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |