Доверительный интервал для математического ожидания нормального распределения при известной дисперсии

Пусть каким-либо образом известна дисперсия 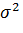генеральной совокупности. Тогда доверительный интервал для математического ожидания определяется как

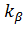причем , где - стандартная ошибка, - квантиль нормального распределения порядка. Квантиль 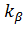есть решение уравнения

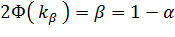
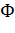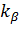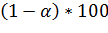где - функция Лапласа. Квантиль может быть определен из таблиц функции Лапласа. Таким образом, можно говорить, что математическое ожидание с вероятностью % лежит в доверительном интервале (118).

Из анализа вышеизложенного следует, что:

· Чем больше объем выборки 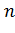, тем выше точность интервального оценивания, так как уменьшается значение интервала ;

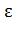· Чем больше значение дисперсии 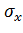, тем ниже точность интервального оценивания, так как увеличивается значение интервала ;

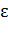· Чем больше значение надежности оценки 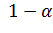, тем ниже точность интервального оценивания, так как увеличивается квантиль 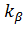и, соответственно, увеличивается значение интервала .

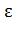Заметим, что правило «трех стандартов» для данного случая представляет собой доверительную оценку истинного значения измеряемой величины 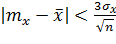с надежностью 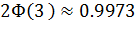независимо от количества измерений.