Проверка однородности дисперсий

Такую операцию приходится выполнять, когда сопоставляются результаты нескольких выборок. Величина рассеяния характеризует такие исключительно важные показатели, как точность машин, приборов, стабильность технологических процессов, качество готовой продукции и т.д. Поэтому, например, о преимуществах той или иной технологии или о качестве выпускаемой продукции можно сделать вывод в результате сравнения дисперсий тех параметров, которые их характеризуют.

Для решения задач такого типа требуется установить, являются ли выборочные дисперсии со степенями свободы и значимо отличающимися или же они характеризуют выборки, взятые из одной и той же генеральной совокупности или из генеральных совокупностей с равными дисперсиями. В этом случае нулевая гипотеза формулируется так: между двумя дисперсиями различия нет при заданном уровне значимости α ( .

Для проверки этой гипотезы используется критерий Фишера, зависящий от числа степеней свободы .

Поскольку для проверки нуль-гипотезы т.е. требуется проверить, что две выработки принадлежат одной и той же генеральной совокупности, то выражение можно представить как отношение выборочных дисперсий

Очевидно, что F всегда больше единицы. Выбирается уровень значимости α. Нулевую гипотезу принимают, если . 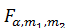определяется по таблицам квантилей F-распределения Фишера для числа степеней свободы и уровня значимости.