Проверка гипотезы о законе распределения

Ранее нами выполнялась проверка гипотез на основании статистических критериев в предположении, что известна функция распределения, которая представлялась нормальным законом распределения Гаусса . Однако в большинстве случаев вид закона распределения не известен и требуется статистическое подтверждение его вида.

Наиболее простым методом проверки согласия результатов эксперимента с тем или иным законом распределения является графический метод. Он заключается в оценке эмпирической функции распределения и сопоставлении ее с функцией предполагаемого теоретического закона. Если построенные экспериментальные точки лежат вблизи теоретического графика, то можно считать, что полученные в опытах данные не противоречат выбранному теоретическому закону распределения. Графический метод является довольно грубой оценкой и может использоваться только на первом этапе исследования.

Проверка гипотезы о законе распределения проводится с использованием специально подобранной статистики. Обычно статистические критерии для проверки таких гипотез называются критериями согласия.

Нулевая гипотеза в данном случае заключается в том, что исследуемая генеральная совокупность не противоречит предполагаемому теоретическому закону распределения. При этом альтернативная гипотеза обычно формулируется как - случайная величина имеет любое другое распределение, отличное от предполагаемого.

Разработано достаточно много критериев согласия, отличающихся как своей мощностью, так и объемом опытных данных, необходимых для их использования. Рассмотрим некоторые из них, и в первую очередь остановимся на критериях согласия, которые могут быть использованы при относительно больших объемах выборки.

Когда экспериментатор располагает достаточно представительным количеством экспериментальных данных ( ), то их предварительная обработка представляет собой упорядочивание экспериментального материала и построение гистограммы. Для этого:

1. Находят наибольшее ( ) и наименьшее ( ) выборочные значения случайной величины и вычисляют ее размах .

2. Размах случайной величины разбивают на равных интервалов, количество которых выбирают в зависимости от объема выборки. Число интервалов к можно определить по формуле с округлением результата до ближайшей целой величины.

3. Определяют ширину интервала , для упрощения расчетов полученные значения округляют в любую сторону, несколько увеличивая или уменьшая при этом размах варьирования .

4. Устанавливают границы интервалов и подсчитывают число попаданий случайной величины в каждый из выбранных интервалов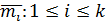

5. Определяют частоту попаданий для каждого интервала как .

6. Определяется величина ординаты , где – вероятность появления случайной величины в 1-м интервале.

7. В системе координат на ширине каждого интервала 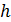откладывают величины | как высоты и строятся прямоугольники.

8. Очевидно, что площадь элементарного прямоугольника Площадь всей гистограммы равна Следовательно, площадь, ограниченная гистограммой, равна единице.

9. Построение интегральной функции распределения осуществляется суммированием вероятностей

Рисунок 4.3.4 – Построение гистограммы и интегральной функции распределения случайной величины

В дальнейшем осуществляется сравнение экспериментально полученного распределения случайной величины с теоретическим. Для этой цели используются различные критерии согласия: Пирсона, Колмогорова и др.

Критерий согласия Пирсона. Является универсальным, т.к. применяется для различных видов распределений. Сущность его состоит в сравнении эмпирических и теоретических частот попадания значений случайной величины в различные интервалы равной длины, на которые разбивается весь диапазон ее возможного изменения. В качестве примера рассмотрим критерий Пирсона о нормальном распределении.

Для стандартного нормального распределения теоретическая вероятность попадания случайной величины в интервал определяется по формуле

.

Отличие оценки закона распределения P от теоретического закона распределения Р* можно охарактеризовать величиной

Где - оценка и теоретическая вероятность случайной величины для i-ого интервала; - весовые коэффициенты, которые с большим весом учитывают отклонения для меньших

Пирсон выбрал весовые коэффициенты следующим образом:

Пирсон показал, что при таком выборе закон распределения слабо зависит отnи P(x), а определяется в основном числом разрядов k (количеством интервалов).

Следовательно,

Очевидно, что при идеальном соответствии экспериментальных данных нормальному закону, экспериментальное значение критерия Пирсона будет равно нулю, т.к. .

Алгоритм использования критерия Пирсона заключается в следующем:

1. Выдвигается нуль-гипотеза: «Отличие экспериментальных данных от нормального закона распределения не существенно» и альтернативная гипотеза: «Отличие экспериментальных данных от нормального закона распределения существенно, т.е. экспериментальные данные не подчиняются закону нормального распределения».

2. По результатам экспериментальных измерений и предположению нормального закона их распределения определяется расчетное значение критерия Пирсона.

3. Определяют число степеней свободы m, задаются уровнем значимости α и определяют теоретическое значение критерия Пирсона .

4. Если , то нуль-гипотеза о нормальном законе распределения экспериментальных данных принимается с доверительной вероятностью В противном случае нуль-гипотеза отвергается и принимается альтернативная.

Критерий согласия Колмогорова. Колмогоров доказал, что независимо от функции распределения вероятностей при неограниченном возрастании числа независимых наблюдений вероятность неравенства стремится к пределу

Значения этой вероятности табулированы.

Суть критерия согласия Колмогорова заключается в следующем. Устанавливается максимальная величина модуля разности между статистической и теоретической функциями распределения вероятностей

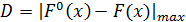
и определяется величина

где n – число независимых наблюдений, и по таблице находится вероятности .

Величина этой вероятности свидетельствует о том, что за счет случайных причин вероятность максимального расхождения между функциями распределения будет не меньше

Если вероятность мала, гипотезу следует отвергнуть, при больших значениях вероятности эту гипотезу следует считать, как не противоречащую опытным данным.