
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи к разделу 4
Задача 4.1. На основании данных, приведенных в таблице 4.3 определить оценку относительной погрешности косвенных измерений
Таблица 4.3.
| № dарианта | Параметр и его обозначение | Формула, по которой определяется параметр | Относительная погрешность факторов, % | Требуется определить |
Расход  
| 
| 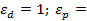 4; 4;
 2; 2;
| 
| |
| Напор в сети Н | 
|  4; 4;
| 
| |
Расход 
| 
|  3; 3;
 2,5; 2,5;
| 
| |
Расход 
| 
| 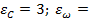 1,5; 1,5;
 4; 4;  2 2
| 
| |
Коэффициент расхода 
| 
|  1,5; 1,5;
 4 4 
| 
| |
Напор в резервуар над центром отверстия 
| 
|  ; ;
 
| 
| |
Давление в трубопроводе 
| 
|  ; ; 
 
| 
| |
Потери напора по длине 
| 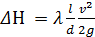
|  ; ; 
| 
| |
Число Рейнольдса 
| 
|  ; ;
 
| 
| |
Потери напора в местных сопротивлениях  
| 
| 

| 
| |
Средняя по сечению скорость 
| 
 
|  ; ; 
| 
| |
Потери напора по длине

| 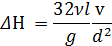
|  ; ;  g – точная величина
g – точная величина
| 
| |
Продолжительность опорожнения вертикального цилиндрического бака 
| 
|  ; ; 
| 
| |
Давление перед насадком 
| 
|  ; ; 
| 
| |
Сила сопротивления трения тонкой прямоугольной пластины, обтекаемой потоком жидкости 
| 
| 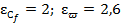 ; ;  g – точная величина
g – точная величина
| 
| |
Опытный коэффициент гидравлического трения 
| 
|  ; ;  g – точная величина
g – точная величина
| 
| |
Расход жидкости через водослив с прямоугольным порогом 
| 
|  ; ;  g – точная величина
g – точная величина
| 
| |
Активный диаметр гидромуфты 
| 
|  ; ; 
| 
| |
Коэффициент момента гидромуфты 
| 
|  ; ; 
| 
| |
Коэффициент мощности гидромуфты 
| 
|  ; ; 
| 
| |
Потери напора по длине 
| 
|  ; ; 
| 
| |
Диаметр трубопровода круглого сечения 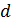
| 
|  ; ;
 ; ;
| 
| |
Площадь эквивалентного сечения шахты 
| 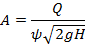
|  ; ; 
| 
| |
Критерий подобия Фруда 
| 
|  ; ; 
| 
| |
Критерий подобия (число)
Эйлера 
| 
|  ; ; 
| 
|
Задача 4.2. Определить оценку для математического ожидания производительности производственной упаковочной линии при ее наладке по следующим измерениям (табл.4.4).
Таблица 4.4
| № вариант | Измерение № 1 | Измерение № 2 | Измерение № 3 | Измерение № 4 | ||||
| Время работы | К-во упак. | Время работы | К-во упак. | Время работы | К-во упак. | Время работы | К-во упак. | |
Задача 4.3. Определить оценку для среднеквадратичного отклонения подачи насоса по результатам измерений (табл. 4.5)
Таблица 4.5
| Вариант | Подача, м3/ч | |||||||
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | |
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | - |
Задача 4.4. В одинаковых условиях проведены испытания центробежного вентилятора до и после реконструкции. Получены равновероятные данные (табл.4.6) о давлении при одинаковой подаче (до и после реконструкции). Провести сравнение результатов испытаний и дать заключение об их различии.
Таблица 4.6
| № варианта | Давление, кПа | |||||
| Номер опыта | ||||||
| 2.2* 2.5 | 1.7 2.1 | 1.9 2.4 | 2.1 1.9 | 2.3 2.2 | 2.0 2.5 | |
| 3.3 3.75 | 2.55 3.2 | 2.85 3.6 | 3.15 2.85 | 3.5 3.3 | 3.0 3.8 | |
| 2.85 3.25 | 2.21 2.7 | 2.47 3.1 | 2.73 2.4 | 2.9 2.9 | 2.6 3.3 | |
| 2.7 3.0 | 2.1 2.5 | 2.3 2.9 | 2.5 2.3 | 2.8 2.7 | 2.4 3.0 | |
| 2.8 3.1 | 2.2 2.6 | 2.4 3.0 | 2.6 2.4 | 2.9 2.7 | 2.5 3.2 | |
| 1.6 1.9 | 1.3 1.6 | 1.4 1.8 | 1.5 1.5 | 1.7 1.8 | 1.5 1.7 | |
| 1.3 1.5 | 1.1 1.3 | 1.2 1.5 | 1.3 1.2 | 1.4 1.4 | 1.2 1.6 | |
| 3.0 3.0 | 2.5 3.0 | 2.8 3.5 | 2.9 2.75 | 3.2 3.3 | 2.7 3.7 | |
| 2.8 3.2 | 2.2 2.6 | 2.3 3.0 | 2.6 2.4 | 2.9 2.8 | 2.5 3.1 | |
| 2.9 3.3 | 2.3 2.8 | 2.5 3.2 | 2.8 2.5 | 3.1 2.9 | 2.7 3.3 | |
| 3.2 3.7 | 2.5 3.1 | 2.8 3.5 | 3.1 2.8 | 3.4 3.4 | 2.9 3.7 | |
| 3.8 4.3 | 2.9 3.6 | 3.3 4.1 | 2.6 3.3 | 4.0 3.8 | 3.5 4.2 | |
| 1.4 1.6 | 1.3 1.7 | 1.5 1.9 | 1.6 1.6 | 1.7 1.8 | 1.5 2.0 | |
| 1.9 2.1 | 1.8 2.2 | 2.0 2.3 | 3.1 3.2 | 3.3 3.4 | 2.1 2.7 | |
| 6.5 7.7 | 6.9 8.1 | 5.7 6.7 | 5.9 6.9 | 6.1 7.2 | 6.0 7.1 | |
| 5.0 5.9 | 5.3 6.2 | 4.4 5.2 | 4.5 5.3 | 4.7 5.5 | 4.8 5.6 | |
| 6.3 7.4 | 6.7 7.8 | 5.5 6.6 | 5.7 6.7 | 5.9 6.9 | 6.1 7.1 | |
| 2.9 3.2 | 2.1 2.6 | 2.2 3.0 | 2.5 2.7 | 2.8 2.8 | 2.6 3.1 | |
| 2.9 3.3 | 2.2 2.8 | 2.5 3.2 | 2.8 2.6 | 3.1 2.9 | 2.7 3.3 | |
| 3.2 3.7 | 2.4 3.1 | 2.8 3.5 | 3.1 2.9 | 3.4 3.4 | 2.9 3.7 | |
| 3.8 4.3 | 2.9 3.6 | 3.2 4.1 | 2.6 3.6 | 4.0 3.8 | 3.5 4.2 | |
| 1.4 1.6 | 1.3 1.7 | 1.5 1.9 | 1.6 1.5 | 1.7 1.8 | 1.5 2.0 | |
| 1.9 2.1 | 1.8 2.2 | 2.1 2.5 | 3.1 3.2 | 3.3 3.4 | 2.1 2.7 | |
| 6.5 7.7 | 6.9 8.1 | 5.6 6.7 | 5.9 7.0 | 6.1 7.2 | 6.0 7.1 | |
| 5.0 5.9 | 5.3 6.2 | 4.4 5.1 | 4.5 5.3 | 4.7 5.8 | 4.8 5.6 |
*Верхняя строка в ячейке – данные до реконструкции, в знаменателе – после реконструкции
Пример решения задачи 4.4. В одинаковых условиях проведены испытания углевыемочного комбайна до и после реконструкции. Получены следующие равновероятные данные для производительности:
до реконструкции 34; 35; 45; 56; 39; 38 т/ч;
после реконструкции 40; 45; 50; 53; 49; 47 т/ч.
Решение. Найдем оценки математических ожиданий для каждой из выборок:

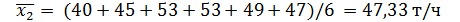
На первый взгляд кажется, что реконструкция привела к существенному увеличению производительности машины - на 14,9%. Проверим достоверность этого утверждения.
Найдем оценки дисперсий выборок:
 (т/ч)2 и
(т/ч)2 и  20,27 (т/ч)2 .
20,27 (т/ч)2 .
Выполним проверку однородности результатов опытов. С этой целью при уровне значимости  0,05 находим доверительный интервал для
0,05 находим доверительный интервал для  и
и  с использованием критерия Стьюдента
с использованием критерия Стьюдента
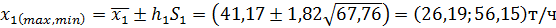

Таким образом, каждая выборка состоит из однородных результатов. Проверим однородность дисперсий. Определим расчетное значение критерия Фишера:
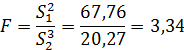
Табличное значение  критерия при уровне значимости
критерия при уровне значимости  = 0,05 и числе степеней свободы числителя и знаменателя
= 0,05 и числе степеней свободы числителя и знаменателя  = 5 составляет 5,05. Так как расчетное значение
= 5 составляет 5,05. Так как расчетное значение  - критерия меньше табличного (3,34 < 5,05), то дисперсии однородны.
- критерия меньше табличного (3,34 < 5,05), то дисперсии однородны.
Определим средневзвешенную дисперсию
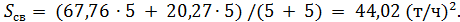
Доверительный интервал для искомой величины
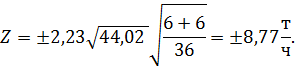
Так как этот интервал включает различие между оценками математических ожиданий


то с вероятностью 0.95 экспериментальный материал не дает оснований утверждать, что реконструкция комбайна привела к значимому увеличению производительности.
Дата добавления: 2014-11-13; просмотров: 253; Мы поможем в написании вашей работы!; Нарушение авторских прав |