
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотез о числовых значениях математических ожиданий
Для решения вопроса о соответствии произведенной продукции определенным требованиям (например, ГОСТ или ТУ), или выявлении преимуществ новой разработки по сравнению с существующими аналогами, возникает необходимость по выборочным средним значениям исследуемых случайных величин делать вывод о соответствующих им генеральных значениях математических ожиданий.
При этом может возникнуть задача (1) сравнения неизвестного математического ожидания  , для которого получена оценка через выборочное среднее
, для которого получена оценка через выборочное среднее  с конкретным числовым значением
с конкретным числовым значением  (например, с известным математическим ожиданием) или задача (2) сравнения двух математических ожиданий
(например, с известным математическим ожиданием) или задача (2) сравнения двух математических ожиданий  и
и  , оцененным по двум выборочным средним
, оцененным по двум выборочным средним  и
и  .
.
В первом случае в качестве нулевой гипотезы выдвигается предположение о том, что оцененное математическое ожидание  равно известному математическому ожиданию М (
равно известному математическому ожиданию М (  ). В качестве альтернативной примем
). В качестве альтернативной примем 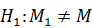
Если генеральная дисперсия  неизвестна и для нее сделана оценка
неизвестна и для нее сделана оценка  , то используется
, то используется  критерий (распределения Стьюдента).
критерий (распределения Стьюдента).  статистика имеет вид:
статистика имеет вид:  . Как и при построении доверительного интервала для математического ожидания, выбирается уровень значимости
. Как и при построении доверительного интервала для математического ожидания, выбирается уровень значимости 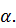 Для числа степеней свободы
Для числа степеней свободы  (c которым сделана оценка дисперсии) устанавливаются границы критической области по табличным значениям квантилей t-распределения. Нулевую гипотезу принимают, т.е. полагают, что
(c которым сделана оценка дисперсии) устанавливаются границы критической области по табличным значениям квантилей t-распределения. Нулевую гипотезу принимают, т.е. полагают, что  при выполнении неравенства:
при выполнении неравенства: 
В задаче (2), где сравниваются два неизвестных математических ожидания  и
и  , прежде всего, необходимо убедиться, что исследуемые выборки независимы между собой. После чего для двух нормально распределенных генеральных совокупностей с неизвестными параметрами
, прежде всего, необходимо убедиться, что исследуемые выборки независимы между собой. После чего для двух нормально распределенных генеральных совокупностей с неизвестными параметрами  которые характеризуются независимыми выборками с объемами, соответственно,
которые характеризуются независимыми выборками с объемами, соответственно,  , для сравнения выборочных средних
, для сравнения выборочных средних  выдвигается нулевая гипотеза о равенстве математических ожиданий:
выдвигается нулевая гипотеза о равенстве математических ожиданий:  Альтернативную гипотезу можем сформулировать как
Альтернативную гипотезу можем сформулировать как 
Как и в предыдущей задаче, используем  критерий. Вид t-статистики зависит от того, равны
критерий. Вид t-статистики зависит от того, равны  , либо не равны
, либо не равны  между собой генеральные дисперсии (для ответа на этот вопрос можно воспользоваться критерием Фишера).
между собой генеральные дисперсии (для ответа на этот вопрос можно воспользоваться критерием Фишера).
В первом случае (когда дисперсии не имеют значимого отличия) статистика принимает вид
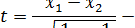
двухвыборочный t-критерий с равными дисперсиями, где  – обобщенное среднее квадратичное отклонение.
– обобщенное среднее квадратичное отклонение.
Во втором случае, когда дисперсии значимо отличаются друг от друга, статистика имеет вид:
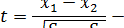
двухвыборочный  критерий с неравными дисперсиями.
критерий с неравными дисперсиями.
В зависимости от условия решаемой задачи выбирается необходимый уровень значимости 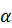 . Границы критической области устанавливаются по табличным значениям квантилей t-распределения. При этом число степеней свободы рассчитывается как
. Границы критической области устанавливаются по табличным значениям квантилей t-распределения. При этом число степеней свободы рассчитывается как  .
.
Нулевую гипотезу принимают при выполнении неравенства 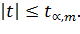
Рассмотрим наиболее типичную практическую задачу. Пусть усовершенствована какая-либо машина. Для оценки полезности реконструкции поставлен сравнительный эксперимент: проведен ряд измерений производительности до и после выполненной модернизации. В результате эксперимента получены две выборки. Первая - число измерений n1 , математическое ожидание 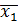
и дисперсия  (до реконструкции). Вторая - число опытов
(до реконструкции). Вторая - число опытов  , математическое ожидание
, математическое ожидание 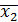 , дисперсия выборки
, дисперсия выборки  (после реконструкции). При этом
(после реконструкции). При этом  . Ставится вопрос: можно ли утверждать, что различие между
. Ставится вопрос: можно ли утверждать, что различие между 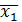 и
и 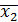 значимо? Иными словами, можно ли утверждать, что реконструкция дала положительные результаты?
значимо? Иными словами, можно ли утверждать, что реконструкция дала положительные результаты?
Обозначим  .
.
Если  выйдет за пределы доверительного интервала
выйдет за пределы доверительного интервала  , то будет значимой величиной.
, то будет значимой величиной.
Предположим, что различие между 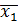 и
и 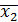 незначимо, т.е. предположим
незначимо, т.е. предположим 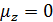 .
.
Тогда доверительный интервал может быть найден как 
Ранее было показано, что для оценки дисперсии косвенный измерений справедлива формула

Для рассматриваемой функции

Так как 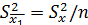 , то
, то 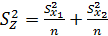
Если  и
и 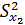 однородны, а только в этом случае можно сравнить
однородны, а только в этом случае можно сравнить  и
и  , то
, то
 или
или 
В результате, искомый доверительный интервал
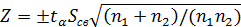
Критерий  берется для соответствующего .уровня значимости и числа степеней свободы
берется для соответствующего .уровня значимости и числа степеней свободы 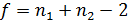 .
.
Если разность математических ожиданий попадает в построенный доверительный интервал, то гипотеза об эффективности модернизации оборудования отвергается. Если разность превышает доверительный интервал, то можно сделать вывод, что результаты имеют существенные различия и реконструкция дала значимый результат.
Дата добавления: 2014-11-13; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |