Проверка однородности нескольких дисперсий

Критерий Фишера используется для сравнения только двух дисперсий, однако на практике приходится сравнивать между собой три и более дисперсий.

При сопоставлении дисперсий ряда выборок нулевая гипотеза заключается в том, что совокупностей, из которых взяты выборки, имеют равные дисперсии. Т.о е. сть проверке подлежит предположение, что все эмпирические дисперсии 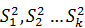относятся к выборкам из совокупности с одной и той же генеральной дисперсией .

Пусть среди выборочных дисперсий обнаружена такая, которая значительно больше всех остальных Задача заключается в том, чтобы выяснить, можно ли считать отличие выделенной дисперсии 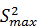существенными. Т.е. Аальтернативная гипотеза может быть выбрана как .

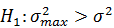При равном объеме выборок 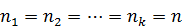для всех выборок может быть использован критерий Кохрена. Статистика критерия Кохрена 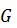рассчитываетка рассчитывается как

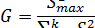
Далее для выбранного уровня значимости α определяется табличное значение этого критерия, который зависит от числа степеней свободы и числа сравниваемых дисперсий : 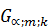. Критическая область строится как . При нулевая гипотеза принимается, т.е. отличие выделенной дисперсии считается несущественной.

В случае подтверждения однородности дисперсий можно сделать оценку обобщенной дисперсии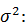

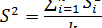
Критерий Кохрена используется только в тех случаях, когда все сравниваемые дисперсии имеют одинаковое число степеней свободы (одинаковые объемы выборок). Если же число измерений в различных сериях неодинаково, то для проверки однородности дисперсий обычно выбирается критерий Бартлета. Введем обозначения для общего числа степеней свободы: 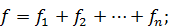и средневзвешенной дисперсии: 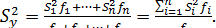Бартлет показал, что в условиях нулевой гипотезы отношение где

распределено приближенно как с степенями свободы, если все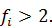

Гипотеза равенства генеральной дисперсии принимается, если

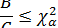
при выбранном уровне значимости .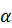

В этом случае различие между выборочными дисперсиями можно считать незначимым, а сами выборочные дисперсии однородными.

Так как 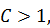если то нулевую гипотезу следует принять. Если 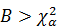, то критерий Бартлета вычисляют полностью.