Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии

В этом случае доверительный интервал для математического ожидания определяется в соответствии с ( ), но значение интервала вычисляется как

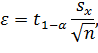
где - выборочное среднеквадратическое отклонение, 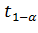- квантиль распределения Стьюдента порядка 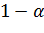и с числом степеней свободы .

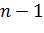При объемах выборки 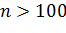вместо квантиля 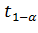можно использовать квантиль нормального распределения 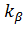, который не зависит от значения объема выборки .

Заметим, что правило «трех стандартов» для данного случая представляет собой доверительную оценку истинного значения 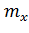измеряемой величины 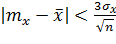с надежностью 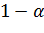, зависящей от количества измерений. Зависимость надежности от количества измерений 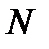представлена в таблице 5.

Таблица 4.1

n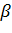
	0.960
	0.985
	0.993
	0.995
	0.997
	0.9973