Двухсторонний доверительный интервал

Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.

В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.

Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.

Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.

Доверительная вероятность –вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.

Оценивание с помощью доверительного интервала– способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.

Рисунок 4.3 - Двухсторонний доверительный интервал

На числовой оси в обе стороны от оценки 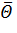строится интервал с границами 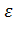, в который оцениваемый параметр попадет с заранее выбранной вероятностью

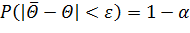(4.1.)

где 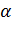- уровень значимости, обычно, 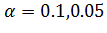или 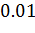. Часто 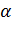выражается в процентах. Уровень значимости связан с доверительной вероятностью (надежностью) формулой

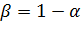(4.2)

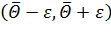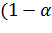Интервал называется двухсторонним доверительным интервалом, который покрывает параметр с надежностью ). Чем меньше значение интервала 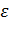для выбранной вероятности 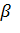, тем точнее оценка параметра . Варианты вычисления доверительных интервалов для оценки математического ожидания и дисперсии рассмотрены в разделе 4.2.3.