
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка точности косвенных измерений
Часто интересующая нас величина непосредственно не может бить измерена, а определяется как функция других величин, которые находятся опытным путем. Например, расход воздуха в прямоугольном канале
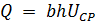
где  - ширина канала, м;
- ширина канала, м; 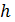 - высота канала, м;
- высота канала, м; 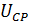 - средняя скорость воздуха, м/с.
- средняя скорость воздуха, м/с.
Для определения расхода измеряют ширину, высоту канала и среднюю скорость воздуха. При измерениях величин  ,
, 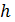 и
и 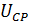 допускаются погрешности. Оценка их может быть выполнена по рассмотренной методике.
допускаются погрешности. Оценка их может быть выполнена по рассмотренной методике.
Погрешность определяемой величины зависит не только от погрешностей измеряемых, но и от вида функциональной связи между ними [4; 6].
Предположим, что величина, погрешность которой необходимо определить является произвольной функцией двух измеряемых переменных х и у:

Подставим ряд параллельных опытов и по полученным данным найдем 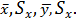
Необходимо определить  Для
Для 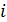 -го измерения
-го измерения 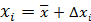 ,
, 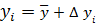 ,
, 
Если функция 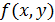 непрерывна и во всех точках интересующего нас интервала и имеет производные, то ее, как известно, можно разложить ряд Тейлора. Выполним эту операцию и оставим в ряде только линейные члены:
непрерывна и во всех точках интересующего нас интервала и имеет производные, то ее, как известно, можно разложить ряд Тейлора. Выполним эту операцию и оставим в ряде только линейные члены:

Так как 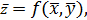 то
то
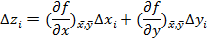
Возведем правую и левую части последнего равенства в квадрат и просуммируем данные по всем измерениям:
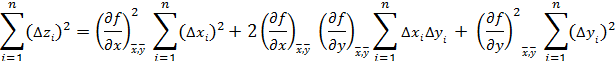
Если закон распределения погрешностей симметричный, например нормальный, то  одинаково часто встречаются как со знаком "+", так и со знаком "-". Поэтому в последнем выражении
одинаково часто встречаются как со знаком "+", так и со знаком "-". Поэтому в последнем выражении
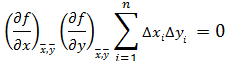
Следовательно,
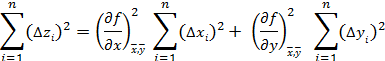
Последнее равенство не нарушится, если все его члены разделить на  .
.
Так как
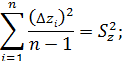
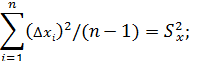

то получим

Пример. Известно, что расход воды через треугольный водослив
 ,
,
где 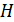 - уровень воды, м.
- уровень воды, м.
Относительная погрешность определения уровня 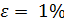 . Определить относительную погрешность расхода.
. Определить относительную погрешность расхода.
В соответствии с полученным выше выражением
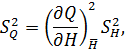
так как
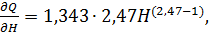
то
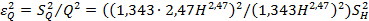
После преобразования имеем
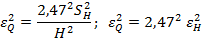
Таким образом, в условиях данного примера 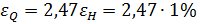


Дата добавления: 2014-11-13; просмотров: 307; Мы поможем в написании вашей работы!; Нарушение авторских прав |