Основы теории случайных процессов и их статистической обработки

Математическое описание стохастических моделей основано на методах теории случайных процессов, корреляционном и спектральном анализе [ ]. Математический аппарат случайных процессов весьма эффективен для исследования функционирования технических систем при наличии случайных внешних воздействий (например, случайное изменение времени, пути, возмущающих нагрузок, координат положения, рельефа обрабатываемых поверхностей, массы и объема перерабатываемых или транспортируемых материалов, жидкостей и т.п.)

Понятие «случайный процесс» является производным от понятия «случайная функция».

Если значение какой-либо функции при данном значении независимой переменной является случайной величиной, то мы имеем случайную функцию.

Случайный процесс - это случайная функция 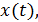независимой переменной в которой является время.

Значения случайной функции 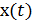в некотором ее сечении при фиксированном аргументе являются случайными величинами, которые описываются вероятностным законом распределения .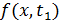

Основные характеристики случайных функций представляются в виде сле-дующих функций: 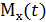- математическое ожидание; - дисперсия; 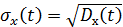- среднее квадратическое отклонение случайной функции, 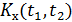- корреляционная функция.

Математическим ожиданием случайной функции 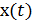называется функция 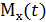, которая при каждом 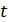представляет собой математическое ожидание соответствующего сечения случайной функции. По смыслу математическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом варьируются конкретные реализации случайной функции.

Дисперсией случайной функции 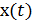называется функция значение которой для каждого 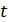равно дисперсии соответствующего сечения случайной функции.

Корреляционной функцией случайного процесса 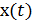называется функция двух аргументов 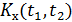, которая для каждой пары фиксированных значений 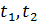равна математическому ожиданию произведения:

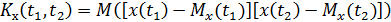
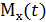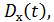
При определении оценок , по экспериментальным данным используются следующие формулы:

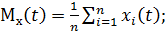
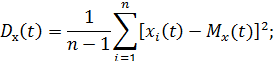
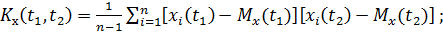
Важным классом случайных функций являются стационарные случайные функции, у которых вероятностные характеристики одинаковы при всех значениях 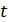. В этом случае математическое ожидание и дисперсия постоянны: , а корреляционная функция зависит только от разности между своими аргументами: где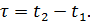

Из симметричности корреляционной функции : следует, что 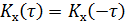, т.е. корреляционная функция стационарной случайной функ-ции есть четная функция аргумента ; поэтому она зависит только от абсо-лютной величины разности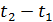

При исследовании параметров технических систем, на которые воздействуют случайные процессы, используются такие типичные корреляционные функции:

1.

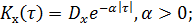
2.

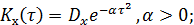
3.

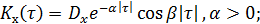
4.

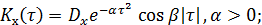
5.

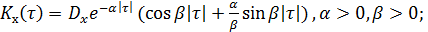
6.

Так указанные функции обладают свойством четности, их графики симметрично относительно оси ординат. Коэффициенты 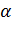и 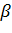подбираются из условия наилучшего приближения опытной кривой методом наименьших квадратов.

На практике вместо корреляционной функции 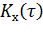часто пользуются безразмерной нормированной корреляционной функцией

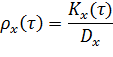
Стационарные случайные процессы обладают свойством эргодичности, которое заключается в том, что отдельная реализация случайного процесса на бесконечном временном интервале полностью определяет весь случайный процесс. В таком случае математическое ожидание, дисперию и корреляционную функцию можно приближенно определять по одной достаточно длинной реализации.

Об эргодичности или неэргодичности стационарного случайного процессаможно судить по его корреляционной функции. Если 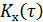стремится к нулю при 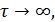то это является достаточным условием для того, чтобы случайный процесс обладал свойством эргодичности.

Благодаря эргодическому свойству значительно упрощаются все расчеты и эксперименты. Вместо ряда параллельных испытаний достаточно воспользоваться одной кривой полученной при испытании в течение достаточно длительного времени.