
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляционная функция
Корреляционная (автокорреляционная) функция стационарного случайного процесса 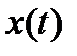 определяется как
определяется как
 . (63)
. (63)
Для двух стационарных случайных процессов 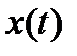 и
и 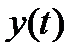 взаимная корреляционная функция определяется как
взаимная корреляционная функция определяется как
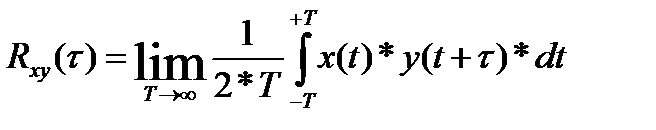 . (64)
. (64)
Для оценки корреляционной функции принято использовать выражение
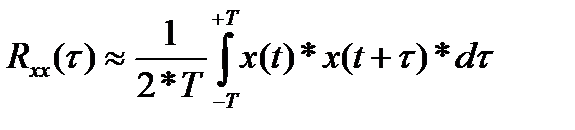 . (65)
. (65)
Пусть имеется запись реализации случайного процесса на интервале наблюдения 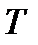 , состоящая из
, состоящая из 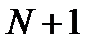 замеров через равные промежутки времени
замеров через равные промежутки времени  . Если придавать
. Если придавать 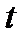 и
и  дискретные значения соответственно
дискретные значения соответственно 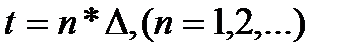 и
и 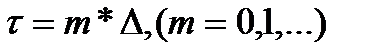 , и обозначить
, и обозначить 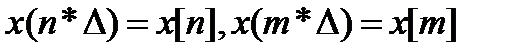 , то оценку (65) можно представить в виде:
, то оценку (65) можно представить в виде:
 . (66)
. (66)
Если ограничиться положительным временем и учесть, что для значений 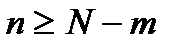 справедливо
справедливо 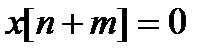 , то оценка корреляционной функции приобретает вид
, то оценка корреляционной функции приобретает вид
 . (67)
. (67)
Аналогичным образом оценивается взаимная корреляционная функция
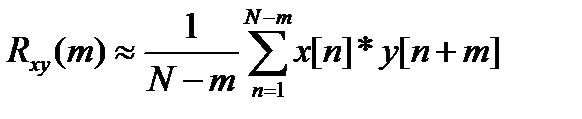 . (68)
. (68)
При проведении эксперимента по оценке корреляционной функции необходимо учитывать следующие рекомендации:
· Выбор интервала дискретности времени  должен удовлетворять условию
должен удовлетворять условию 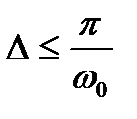 , где
, где  - ожидаемая наивысшая частота спектра сигнала
- ожидаемая наивысшая частота спектра сигнала  ;
;
· Выбор максимального значения интервала корреляции должен удовлетворять условию  ,
,
где 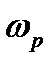 - низшая частота спектра сигнала
- низшая частота спектра сигнала  ;
;
· Выбор интервала наблюдения должен удовлетворять условию 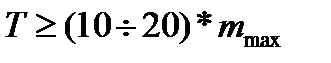 .
.
Дата добавления: 2014-11-13; просмотров: 319; Мы поможем в написании вашей работы!; Нарушение авторских прав |