Назначение и сущность метода; гипотеза фильтра

Метод гармонической линеаризации

Поскольку этот метод является приближённым, то полученные результаты будут близки к истине только при выполнении определённых допущений:

1. Нелинейная система должна содержать только одну нелинейность;
2. Линейная часть системы должна представлять собой фильтр низких частот, ослабляющий высшие гармоники, возникающие в предельном цикле;
3. Метод применим только к автономным системам.

Назначение и сущность метода; гипотеза фильтра

Метод позволяет исследовать возможность появления автоколебательных режимов, определить основные параметры автоколебаний (A, ω_а),

качественно оценить влияние нелинейностей на устойчивость и переходные процессы в системе, как устранить автоколебания или же как изменить их параметры в желаемом направлении.

Сущность метода гармонического баланса заключается в замене нелинейного элемента эквивалентным линейным, передаточный коэффициент которого не является постоянным, а зависит в общем случае от амплитуды и частоты искомых автоколебаний.

Рассматривается замкнутая система с одним НЭ (рис. 5.35). Изучается свободное движение системы, то есть движение при ненулевых начальных условиях в отсутствие внешних воздействий. В системе возможно возникновение автоколебаний. При этом z(t)- периодическая функция, содержащая спектр гармонических составляющих.

		y(t)
		z(t)
			Wл(p)

Рис. 5.35. Структурная схема системы с одним нелинейным элементом

Если при прохождении через линейную часть системы z(t) фильтруется так, что можно пренебречь всеми гармониками выше первой, то анализ системы можно вести методом гармонического баланса. Это предположение- необходимое условие применения метода гармонической линеаризации, его называют гипотезой фильтра, введено Е.П. Поповым. Поскольку высшие гармоники по амплитуде обычно меньше, чем первая гармоника, а линейная часть САУ узкополосная, устойчивая (могут быть нулевые корни характеристического уравнения линейной части), отсутствуют резонансные звенья, |W(jω_a)| >>|W(jkω_a)| при k >1, то во многих практических случаях гипотеза фильтра выполняется. Для приближённых расчётов последнее условие может быть смягчено и сформулировано так: наклон ЛАЧХ линейной части должен быть по крайней мере от -20 до -40 дБ/дек на частоте автоколебаний ω_а и выполнены неравенства:

при наклоне ЛАЧХ , ,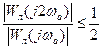

-20 дБ/дек

при наклоне ЛАЧХ , .

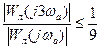-40 дБ/дек