Гармоническая линеаризация НЭ

При гармонической линеаризации нелинейные элементы заменяются их линейными моделями, полученными в результате изучения реакций на гармонические входные сигналы.

На вход нелинейного элемента подаётся гармонический сигнал ε(t)=A·sinωt , выходная функция z(t)=F(A·sinωt)- периодический (не гармонический) сигнал (рис. 5.36).

Ограничимся рассмотрением безынерционных НЭ с петлевыми нечётносимметричными статическими характеристиками (простейшие НЭ).

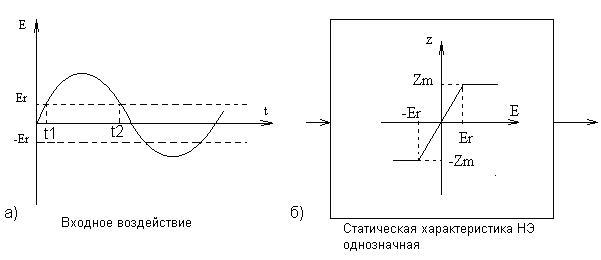
Рис.5.36. Преобразование входного гармонического

сигнала простейшим НЭ

Разложим z(t) в ряд Фурье

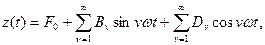(5.72)

где при усреднении по фазе и замене

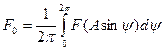- постоянная составляющая выходной функции,

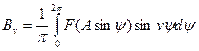- амплитуда синфазной составляющей z(t),

- амплитуда квадратурной составляющей z(t).

Выходной сигнал НЭ может быть представлен своей первой гармоникой, так как статическая характеристика НЭ нечетная ( 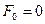) и выполняется гипотеза фильтра:

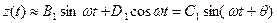, (5.73)

где , .

Сделав замену 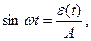получим

, где 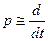- оператор (5.74) дифференцирования по времени,

- коэффициенты гармонической линеаризации НЭ.

Преобразования по Лапласу выходной функции и входного воздействия имеют вид

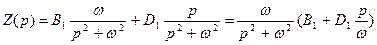, (5.75)

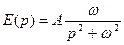, где р – оператор Лапласа.

По аналогии с линейным звеном свойства нелинейного элемента можно представить передаточным коэффициентом, называемым эквивалентным комплексным передаточным коэффициентом НЭ (эквивалентной передаточной функцией, описывающей функцией).

Определим эквивалентную передаточную функцию:

, (5.76)

преобразование Фурье 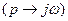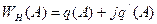- эквивалентная частотная функция, которая зависит от амплитуды входного сигнала.

Таким образом, нелинейный элемент может быть заменен линейным; этот прием получил название гармонической линеаризации нелинейностей.

Эквивалентная структурная схема НЭ приведена на рис. 5.37.

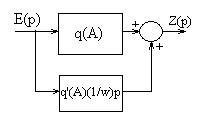
Рис. 5.37. Эквивалентная структурная схема НЭ

Если статическая характеристика НЭ однозначная (не петлевая), то .

Наряду с рассмотренными встречаются такие нелинейные элементы, у которых выходной сигнал является функцией входного воздействия и его производной, т.е. z=F(Asinψ, Aωcosψ). В таких случаях первая гармоника периодических колебаний на выходе зависит не только от амплитуды, но и от частоты синусоидальных колебаний на входе.

Приведём операторную запись во временной области, используя эквивалентный оператор нелинейного элемента:

z=[q(A,ω) + q´(A,ω)· 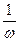·p] ·ε , где p≡ . (5.77)

Такие элементы называются непростейшими. Коэффициенты гармонической линеаризации оказываются зависимыми не только от амплитуды, но и от частоты и в случае нескольких простейших нелинейных элементов, между которыми располагаются инерционные звенья.