Построение кривой переходного процесса по фазовой траектории

Для построения процессов по интересующему отрезку фазовой траектории требуется определить время движения изображающей точки отрезка фазовой траектории. Зафиксируем интересующий нас отрезок AB фазовой траектории 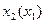, как это показано на рис. 5.46.

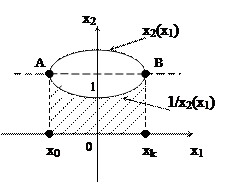
Рис. 5.46. Отрезок AB фазовой траектории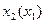

Найдём, за какое время 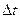изображающая точка пройдёт от начала отрезка AB 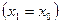до его конца .

По определению имеем

,

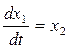отсюда следует

.

Интегрируя, получим

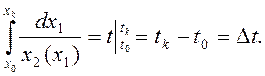(5.89)

Результат имеет простой геометрический смысл – время процесса (перехода системы из одного состояния в другое) пропорционально площади под кривой 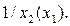Чем выше проходит траектория 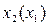в верхней полуплоскости, а значит, чем больше скорость процесса, тем ближе кривая 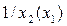к оси абсцисс, тем меньше 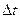, т.е. быстрее протекает процесс.

Пусть имеется фазовая траектория системы. Известно, что значение координаты y во времени будет или .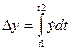

Отсюда .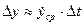

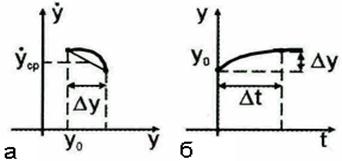
Рис. 5.47. Аппроксимация фазовой траектории прямолинейным отрезком (а) и начальный

участок временной характеристики (б)

Фазовая траектория аппроксимируется прямолинейными отрезками и определяются значения 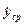в середине каждого отрезка (рис. 5.47). Проекция этого отрезка на ось y даёт .

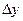При этом

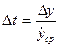и .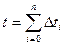

Методика аппроксимации фазовой траектории прямолинейными отрезками и построения временной характеристики показаны на рис. 5.49.

Рис. 5.48. Фазовая траектория и соответствующая ей

временная характеристика системы

Методы вычисления времени по фазовой траектории имеют существенный недостаток: трудность точного считывания координат кривой.

Рассмотрим пример фазовой траектории в виде отрезка прямой, направленной к началу координат (рис. 5.49,а).

Рис. 5.49. Фазовая траектория и переходный процесс

Уравнение отрезка прямой:

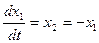. (5.90)

Обратная кривая

- отрезок гиперболы;

площадь под ней равна времени переходного процесса – прихода изображающей точки в начало координат.

Найдём это время:

.

Действительно, прямолинейному отрезку фазовой траектории соответствует экспоненциальное движение (рис. 5.49,б), т.е. решение дифференциального уравнения (5.90) при начальном условии 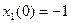имеет вид

.

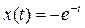Такое движение затухает бесконечно долго.