Имитационное моделирование нелинейных систем

1. Исследование нелинейных систем методом гармонического баланса (методом описывающей функции).

Условия применения метода:

1. Расчетная модель нелинейной системы имеет только одну нелинейность;

2. Выполняется гипотеза фильтра – линейная часть системы является фильтром низких частот;

3. Система автономна, т.е. стационарна и свободна (входной сигнал системы равен нулю).

1.1. Исследование нелинейной САУ, содержащей идеальное реле (компаратор).

Структурная схема системы приведена на рис. 5.53.

Рис. 5.53. Структурная схема САУ, содержащей идеальное реле

Примем V = 1.

1.1.1. Анализ работы нелинейной системы по методу Л. С. Гольдфарба.

По этому методу условие гармонического баланса выражено уравнением

Л. С. Гольдфарба

, (5.91)

где Wн(A) – эквивалентный комплексный передаточный коэффициент НЭ (описывающая функция),

. (5.92)

1.1.1.1. Построим в MATLAB амплитудно-фазовую характеристику линейной части системы и график функции

, (5.93)

так как описывающая функция идеального реле

. (5.94)

Скрипт MATLAB:

% Исследование нелинейной системы по методу Л.С.Гольдфарба

% График АФХ линейной части нелинейной системы

num=[4];den=[1 2 1 0];

sys=tf(num,den);

nyquist(sys)

MATLAB возвращает график, приведенный на рис. 5.54.

Рис. 5.54. График АФХ линейной части нелинейной системы

1.1.1.2. Определим точку пересечения графиков (в ней выполняется условие гармонического баланса) и рассчитаем частоту, период и амплитуду автоколебаний в системе.

% Расчёт амплитуды и периода автоколебаний

V=1; w=1.01;

d=-1.97;

A=-4*V*d/pi

T=2*pi/w

>>

A =

2.5083

T =

6.2210

Таким образом, в системе возникают автоколебания с параметрами: ω=1.01 с^-1, A=2.508, Т= 6.2210 с.

1.1.2. Анализ работы нелинейной САУ по методу А.А. Вавилова.

Условия баланса амплитуд и фаз, записанные в логарифмической форме, имеют вид

L_Л(ω) = - L_H(A);

Θ_Л(ω) + Θ_Н(А) = (2k+1)π, k=0,1,2,… . (5.95)

1.1.2.1. Построим в MATLAB функции: Θ_Л(ω) =-π/2-2*arctg(ω), Θ_Н(А) =0,

и (5.96)

Скрипт MATLAB:

% Исследование нелинейной системы по методу А.А.Вавилова

% Графики ЛЧХ линейной части нелинейной системы; для получения графика –L_н(А)

% строим модель sys1, где ω=А

num=[4];den=[1 2 1 0];

sys=tf(num,den);

V=1;

num1=[-pi/(4*V) 0]; den1=[1];

sys1=tf(num1,den1);

bode(sys,sys1)

MATLAB возвращает графики, приведенные на рис. 5.55.

Рис. 5.55. Графики ЛЧХ линейной части НС и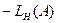

1.1.2.2. Определяем частоту, амплитуду и период предполагаемых автоколебаний по графику:

Θ_Л(ω) + Θ_Н(А) = - π ( здесь k = 0) 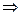ω=1.01 c^-1, А=2.5, Т=6.2210 с.

1.1.3. Аналитическое описание объекта управления в пространстве состояния.

Составим векторно-матричную форму уравнения состояния по передаточной функции объекта:

(5.97)

Скрипт MATLAB:

% Определение параметров матриц уравнения состояния объекта

% по его передаточной функции

num=[4];den=[1 2 1 0];

sys_tf=tf(num,den)

sys_ss=ss(sys)

Результаты расчёта система выводит в «Окно команд»:

>>

Transfer function:

---------------

s^3 + 2 s^2 + s

a =

x1 x2 x3

x1 -2 -0.5 0

x2 2 0 0

x3 0 1 0

b =

u1

x1 1

x2 0

x3 0

c =

x1 x2 x3

y1 0 0 2

d =

u1

y1 0

Continuous-time model.

>>

1.1.4. Исследование модели системы в Simulink по рис. 5.56.

Производим набор модели системы в Simulink по рис. 5.56.

.Рис. 5.56. Модель системы в Simulink

Вводим параметры матриц, полученные в пункте 1.1.3 и, задав начальные условия

[0;0;1.5], запускаем модель; в окне Scope по графику y(t) (рис. 5.57)

Рис. 5.57. График выходной функции системы

определяем параметры устойчивых автоколебаний: ω=0,97 c^-1, А=2.6, Т=6.5 с.

Результаты исследования моделей системы различными методами идентичны.

1.2. Исследование нелинейной системы автоматического управления, содержащей нелинейность типа “люфт”.

1.2.1. Структурная схема САУ с люфтом приведена на рис. 5.58.

Рис. 5.58. Структурная схема САУ с люфтом

Необходимые условия применимости метода гармонического баланса в нелинейной системе при r(t) = 0 выполняются.

1.2.2. Проведём анализ работы нелинейной системы по методу Л. С. Гольдфарба.

Нелинейность типа “люфт” вносит отставание по фазе.

Описывающая функция для “люфта” имеет вид

A > C ; (5.98)

(5.99)

Численные значения частотной передаточной функции

(5.100)

и функции -1/ приведены в таблице 5.2.

Таблица 5.2

Численные значения и

A	-1/		ω
	¥	—	—
1,11			0,3
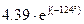
1,25			0,41
1,67		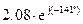	0,65
2,50			0,86
3,75
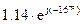
			1,12
			1,27

По табличным данным выявлены режимы автоколебаний, их параметры и устойчивость:

y₁(t)=1.25sin0.41t – неустойчивые автоколебания, y₂(t)=3.75sint – устойчивые автоколебания.

1.2.3. Проведём исследование нелинейной системы в MATLAB.

1.2.3.1. Определим параметры матриц уравнения состояния объекта управления.

Скрипт MATLAB:

% Определение параметров матриц ОУ

num=[4];den=[1 3 2 0];

sys_tf=tf(num,den)

sys_ss=ss(sys_tf)

Результат расчёта:

>>

Transfer function:

-----------------

s^3 + 3 s^2 + 2 s

a =

x1 x2 x3

x1 -3 -0.5 0

x2 4 0 0

x3 0 8 0

b =

u1

x1 0.25

x2 0

x3 0

c =

x1 x2 x3

y1 0 0 0.5

d =

u1

y1 0

Continuous-time model.

>>

Производим набор схемы моделирования системы с люфтом в Simulink (рис. 5.59).

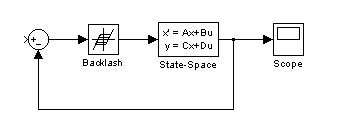
Рис. 5.59. Схема модели системы с люфтом в Simulink

Вводим в модель параметры элементов и начальные условия [0;0;10]. Результат моделирования в окне Scope имеет вид, приведенный на рис. 5.60.

Рис. 5.60. Реакция модели нелинейной системы на начальные условия [0;0;10]

При вводе в модель начальных условий [0;0;6] переходный процесс имеет форму расходящихся колебаний до установившегося режима в виде автоколебаний (рис. 5.61).

Рис. 5.61. Реакция модели нелинейной системы на начальные условия [0;0;6]

Модель иллюстрирует наличие устойчивого предельного цикла y(t)=3.52sin1.01t.

2. Исследование нелинейных САУ методом фазовых траекторий.

2.1. Математическое описание системы стабилизации положения спутника приведено в примере 5.15.

Методика анализа нелинейной системы (рис. 5.51) заключается в построении множества фазовых траекторий движения системы в пространстве состояний с двумя координатами x₁ и x₂. Фазовый портрет содержит исчерпывающую информацию о поведении системы при различных начальных условиях.

Определим матрицы уравнения состояния спутника по скрипту MATLAB:

% Определение параметров матриц уравнения состояния спутника

num=[1];den=[1 0 0];

sys_tf=tf(num,den)

sys_ss=ss(sys_tf)

>>

Transfer function:

---

s^2

a =

x1 x2

x1 0 0

x2 1 0

b =

u1

x1 1

x2 0

c =

x1 x2

y1 0 1

d =

u1

y1 0

Continuous-time model.

>>

2.2. Построим модель системы в Simulink и введём в модуль объекта рассчитанные параметры матриц и начальные условия (рис. 5.62).

Рис. 5.62. Модель системы стабилизации спутника в Simulink

При моменте инерции спутника J=150 кгм² примем u=m_вр/J = 0.12 Н/кгм и начальные условия [0.2;-0.05].

2.3. Исследование модели системы по фазовым траекториям при величине передаточного коэффициента датчика скорости равном нулю иллюстрируется графиком, приведенным

на рис. 5.63.

Рис. 5.63. График фазовой траектории системы при k_дс=0

Если величина передаточного коэффициента датчика скорости k_дс=0.278, система работает устойчиво без скользящего режима (рис. 5.64).

Рис. 5.64. График фазовой траектории системы при k_дс=0.278

Скользящий режим работы системы наблюдается при k_дс 1.

Если наклон линии переключения является малым, то по мере приближения траектории к началу координат она всегда стремится пересечь линию переключения независимо от того, по какую сторону от нее находится. Это приводит к тому, что фазовая траектория скользит вдоль линии переключения к началу координат.

График фазовой траектории при k_дс=1.01 приведен в окне осциллографа «XY Graph»

(рис. 5.65).

.

Рис. 5.65. График фазовой траектории системы при k_дс= 1,01

ЛИТЕРАТУРА

1. Арнольд В.И. Теория катастроф.-М.: Наука, 1990.

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. СПб, Изд-во “Профессия”, 2003.

3. Дьяконов В.П. MATLAB 6/6.1/6.5+Simulink 4/5 в математике и моделировании.- М.:

СОЛОН-Пресс, 2003.

3. Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах: Учеб.

пособие.-М.: Высшая школа, 2003.

5. Ротач В.Я. Теория автоматического управления: Учебник для вузов.- 2-е изд., перераб. и доп.- М.: Издательство МЭИ, 2004.

6. Теория автоматического управления: Учеб. для вузов/ С.Е. Душин, Н.С. Зотов,

Д.Х. Имаев и др.; Под ред. В.Б. Яковлева.-М.: Высшая школа, 2003.

7. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования: Учеб. пособие для втузов.-М.: Машиностроение, 1989.

8.Филлипс Ч., Харбор Р. Системы управления с обратной связью.- М.: Лаборатория Базовых Знаний, 2001.