Анализ работы нелинейных систем по методу А.А.Вавилова

Условие баланса амплитуд и фаз, записанные в логарифмической форме:

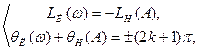
(5.84)

позволяют просто и наглядно графически определить частоту и амплитуду автоколебаний в системе, а также их устойчивость.

Пример 5.12.

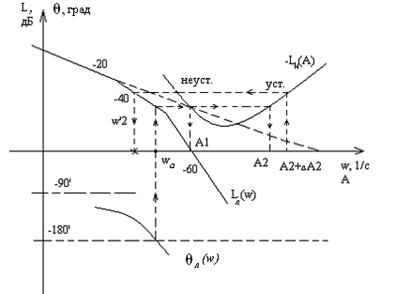Рис. 5.42. ЛЧХ линейной

части системы и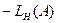

Условия гармонического баланса могут выполняться лишь в зоне частот, где 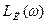>0 и 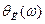= 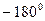(рис. 5.42).

При 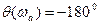( 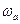- частота предполагаемых автоколебаний) 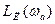= 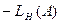при двух значениях А: 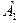и 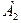.Режим автоколебаний ( 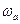, 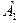) – неустойчивый, режим ( 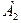, 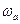) – устойчивый.

При исследовании устойчивости периодических решений по ЛЧХ следует пользоваться критерием Найквиста. Если под действием возмущения амплитуда колебаний режима ( 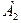, 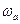) увеличилась на величину , то, приняв в качестве частоты среза 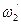, определяем, что система устойчива, иначе неустойчива 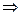автоколебания рассматриваемого режима устойчивые.

При определённых условиях влияние высших гармоник на входе нелинейных элементов и малых параметров, обусловленных погрешностями идентификации нелинейных элементов и линейной части и малыми вариациями параметров системы в процессе эксплуатации, может приводить к существенному изменению амплитуды и частоты периодических решений.

Наличие звеньев с существенными нелинейностями в САУ, не предусмотренных структурой, может вызвать ухудшение качества управления, а в ряде случаев делает управление невозможным. Это проявляется в росте погрешности управления, увеличении времени 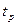, колебательности переходного процесса, потере системой устойчивости в большом, возможности возникновения автоколебательных режимов.

Способы уменьшения влияния нелинейных элементов:

1. Улучшение конструкции функциональных элементов;
2. Изменение линейной части (изменение параметров и структуры линейной части; введение дополнительных линейных обратных связей-охват нелинейных элементов линейной обратной связью);
3. Компенсация влияния нелинейностей (применение специальных компенсирующих нелинейных элементов, обеспечивающих линеаризацию системы; введение дополнительных сигналов управления по отклонению);
4. Вибрационная линеаризация нелинейностей.