
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение фазовых траекторий
САУ называется автономной, если при рассматриваемых процессах она не подвергается внешним воздействиям и не содержит параметров, изменяющихся во времени.
Если в дифференциальное уравнение второго порядка автономной системы
 (5.85)
(5.85)
 подставить
подставить
то оно может быть записано в форме системы двух дифференциальных уравнений первого порядка:
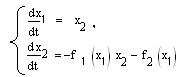 (5.86)
(5.86)
.
Разделив почленно уравнения, получим
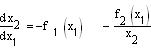
, (5.87)
решение которого-уравнение фазовой траектории.
Фазовая траектория в декартовой системе координат x1,x2 есть интегральная кривая дифференциального уравнения (5.87) при заданных начальных условиях: x1(t0) и x2(t0).Проинтегрировав это уравнение, находим уравнение интегральной кривой
x2=f3(x1,c) на фазовой плоскости, где с-постоянная интегрирования, определяемая из начальных условий.
Точки (x1,x2) , в которых наклон траектории не определен, называются особыми.
При построении фазовых траекторий удобно пользоваться методом изоклин:

положим наклон
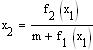 -
-
тогда из (5.87) получим - уравнение линии, в любой из точек которой фазовая
траектория имеет один и тот же угол наклона, т.е. будет уравнением изоклины.
На фазовой плоскости наносят семейство изоклин для различных значений m, после чего вдоль каждой изоклины вычерчивают ряд параллельных отрезков с углом наклона α (tgα=m). Фазовая траектория получается построением плавной кривой, пересекающей каждую изоклину под соответствующим углом.
Примеры фазовых траекторий; особые линии и особые точки на фазовых портретах приведены на рис. 5.43.

Рис. 5.43. Особые линии и особые точки на фазовых портретах
Если модель системы содержит нелинейный элемент с кусочно-постоянной (или кусочно-линейной) характеристикой, то процесс может быть разбит на ряд интервалов так, что в пределах каждого интервала движение описывается линейными дифференциальными уравнениями. На фазовой плоскости каждому линейному участку такой характеристики нелинейного элемента соответствует отдельная область или лист, в пределах которого правые части дифференциальных уравнений линейны, а фазовые траектории составлены из дуг траекторий линейных систем. Излому или разрыву таких статических характеристик нелинейных элементов соответствует граница листа фазовой траектории (линия переключения).
Пример 5.13. Пусть исходная модель нелинейной системы преобразована к виду, изображенному на рис. 5.44.
 |
Рис. 5.44. Структурная схема релейной САУ
Требуется провести анализ нелинейной системы по методу фазовых траекторий.
Анализ системы проводится по фазовому портрету, методика построения которого следующая.
Запишем дифференциальные уравнения системы в форме Коши. Выберем следующие переменные состояния:
 ;
;
 .
.
Дифференциальное уравнение линейной части

с учетом  запишется так:
запишется так:
 .
.
Отсюда получаем требуемую систему уравнений состояния:
 ;
;
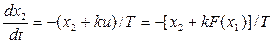 .
.
Поделим второе уравнение на первое:
 . (5.88)
. (5.88)
Если учесть, что на различных интервалах 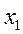 функция F(
функция F(  ) постоянна, то в уравнении (5.88) разделяются переменные, т.е. имеем:
) постоянна, то в уравнении (5.88) разделяются переменные, т.е. имеем:
 .
.
Интегрирование последнего уравнения даёт
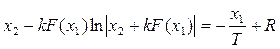 ,
,
где R –постоянная, определяемая начальными условиями.
Для различных интервалов  получим следующие уравнения для фазовых траекторий:
получим следующие уравнения для фазовых траекторий:
 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
Для нелинейного элемента типа «реле с зоной нечувствительности» положение равновесия:  на входе интегратора в равновесном состоянии
на входе интегратора в равновесном состоянии  .
.
Этому режиму работы системы соответствует отрезок равновесия на фазовом портрете.
Фазовый портрет релейной системы «с зоной нечувствительности» показан на рис. 5.45. Линиям переключения реле  соответствуют границы трёх «листов» фазовой плоскости. Движение системы завершается на отрезке равновесия.
соответствуют границы трёх «листов» фазовой плоскости. Движение системы завершается на отрезке равновесия.

Рис. 5.45. Фазовый портрет нелинейной системы с нелинейным
элементом типа «реле с зоной нечувствительности»
Пример 5.14. Фазовый портрет системы первого порядка, рассмотренной в примере 5.13, представляет собой единственную кривую:
 ,
,
проходящую через начало координат и располагающуюся во втором и четвёртом квадрантах при условии 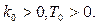 Во втором квадранте (
Во втором квадранте (  ) изображающая точка движется в сторону увеличения значений x, а в четвёртом
) изображающая точка движется в сторону увеличения значений x, а в четвёртом  - в сторону уменьшения значений x, т.е. при любых начальных условиях изображающая точка движется к началу координат, поэтому положение равновесия устойчивое асимптотическое в целом (система абсолютно устойчива).
- в сторону уменьшения значений x, т.е. при любых начальных условиях изображающая точка движется к началу координат, поэтому положение равновесия устойчивое асимптотическое в целом (система абсолютно устойчива).
Дата добавления: 2015-01-29; просмотров: 1602; Мы поможем в написании вашей работы!; Нарушение авторских прав |