Идеальный релейный элемент.

Так как нелинейный элемент безынерционный (рис. 5.38), то коэффициенты гармонической линеаризации от не зависят и от усреднения по времени можно перейти к усреднению по фазе.

Рис.5.38. Преобразование входного синусоидального воздействия идеальным

релейным элементом

Вычислим коэффициенты гармонической линеаризации:

,

,

.

Эквивалентная амплитудная характеристика идеального реле равна :

,

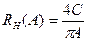а фазовые сдвиги , т.е. фаза первой гармонической составляющей выхода совпадает с фазой входа.

График эквивалентной амплитудной характеристики показан на рис.5.39, из которого видно, что малые по амплитуде сигналы проходят с большим усилением, а большие – с малым (дискриминация сигналов по уровню, рис.5.40).

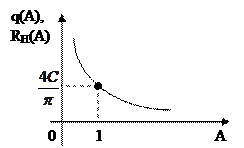
Рис. 5.39. График зависимости эквивалентного усиления идеального реле от

амплитуды гармонического сигнала

Рис. 5.40. Отображение модели идеального релейного элемента в модель звена с

дискриминацией сигналов по уровню

Коэффициенты гармонической линеаризации типовых безынерционных нелинейных элементов приведены в табл. 5.1.

Таблица 5.1