Методика изучения числовых равенств и неравенств

Понятия о равенствах, неравенствах и уравнениях раскрываются во взаимосвязи. Работа над ними ведется с I класса, органически сочетаясь с изучением арифметического материала.

Программа по математике для I—III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений «больше», «меньше», «равно»; научить записывать результаты сравнения с помощью знаков «>», « О , « = » и читать полученные равенства и неравенства.

Числовые равенства и неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками «>», «<», « = » соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Два равных числа или два выражения, имеющие равные значения, соединенные знаком « = », образуют равенство. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о в е р н ы х равенствах и неравенствах.

Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.

Ознакомление с равенствами и неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.

С р а в н е н и е чисел осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка (см. главу II, с. 60). Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют п е р е д числом 10; 5 больше, чем 4, потому что при счете число 5 называют п о с л е числа 4.

Установленные отношения записываются с помощью знаков «>», «<», « = », учащиеся упражняются в чтении и записи равенств и неравенств.

Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).

С р а в н е н и е в е л и ч и н сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I—III классах предлагать разнообразные упражнения, например:

1) подберите равную величину: 7 км 500 м = ? м, 3080 кг = ? т ? кг.

2) Подберите числовые значения величин так, чтобы запись была верной: ? ч<? мин, ? см=? дм ? см, ? т ? ц=? кг.

3) Вставьте наименования у величин так, чтобы запись была верной: 35 км = 35000 ..., 16 мин>16 ..., 17 т 5 ц = 17500 ... .

4) Проверьте, верные или неверные равенства даны, исправьте знак, если равенства неверны: 4 т 8 ц=480 кг, 100 мин = 1 ч, 2 м 5 см = 250 см.

Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.

Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в с р а в н е н и и в ы р а ж е н и я и ч и с л а (числа и выражения). Первые неравенства вида 3+1 > 3 , 3—1 < 3 полезно получать из равенства (3 = 3), сопровождая преобразования соответствующими операциями над множествами. Например, на классном наборном полотне и на партах отложено 3 треугольника и 3 кружка и записано: 3=3. Учитель предлагает детям придвинуть к 3 треугольникам еще 1 треугольник и записать это (3+1—запись под треугольниками). Число кружков не уменьшилось (3). Учащиеся сравнивают число треугольников и кружков и убеждаются, что треугольников больше, чем кружков (4>3), значит, можно записать: 3+1 > 3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3—1<3 (три минус один меньше, чем три).

В дальнейшем выражение и число (число и выражение) учащиеся сравнивают, не прибегая к операциям над множествами; находят значение выражения и сравнивают его с заданным числом, что отражается в записях:

5 + 3 > 5 2<7—4 7 = 4 + 3

8 > 5 2<3 7 = 7

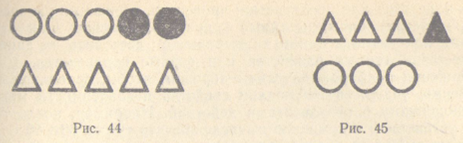
После знакомства с названиями выражений учащиеся читают равенства и неравенства так: сумма чисел 5 и 3 больше, чем число 5; число 2 меньше, чем разность чисел 7 и 4, и т. п.

Опираясь на операции над множествами и сравнение множеств, учащиеся практически усваивают важнейшие свойства равенств и неравенств (если а = Ь, то Ь = а\ если а>Ь, то Ь<а).

Дети видят, что если кружков и треугольников поровну (рис. 44), то можно сказать, что кружков столько, сколько треугольников (3 + 2 = 5), а также треугольников столько, сколько кружков (5 = 3 + 2). Если же предметов не поровну (рис. 45), то одних — больше ( 3 + 1 > 3 ) , а других меньше ( 3 < 3 + 1 ).

В дальнейшем при изучении действий в пределах 100, 1000 и 1 000 000 упражнения на сравнение выражения и числа даются на новом числовом материале и увеличивается количество чисел и знаков действий в выражениях.

Сравнивая неоднократно специально подобранные выражения и числа, например: 17+0 и 17, 19 — 0 и 19, 7-1 и 7, 0:5 и 0, с+1 и с, с:1 и с и т. п., учащиеся накапливают наблюдения об особых случаях действий, глубже осознают конкретный смысл действий. Упражнения на сравнение выражений и числа закрепляют умения читать выражения и способствуют выработке вычислительных навыков.

С р а в н и т ь д в а в ы р а ж е н и я — значит, сравнить их значения. Сравнение выражений впервые включается уже в конце изучения сложения и вычитания в пределах 10, а затем при изучении действий во всех концентрах эти упражнения систематически предлагаются учащимся. Например, надо сравнить суммы: 6 + 4 и 6 + 3. Ученик рассуждает так: первая сумма равна 10, вторая — 9, 10 больше, чем 9, значит, сумма чисел 6 и 4 больше, чем сумма чисел 6 и 3. Это рассуждение отражается в записях:

6 + 4 > 6 + 3 7—5<7—3 4 + 4 = 1 0 - 2

10>9 2 < 4 8 = 8

При изучении действий в других концентрах упражнения на сравнение выражений усложняются: более сложными становятся выражения, учащимся предлагаются задания вставить в одно из выражений подходящее число так, чтобы получить верные равенства или неравенства; проверить, верные ли равенства (неравенства) даны, неверные исправить, изменив знак отношения или число в одном из выражений; составить из данных выражений верные равенства или верные неравенства. Сами выражения подбираются таким образом, чтобы, сравнивая вы ражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60 + 40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.

Таким образом, при изучении всех концентров упражнения на сравнение чисел и выражений, с одной стороны, способствуют формированию понятий о равенствах и неравенствах, а с другой стороны, усвоению знаний о нумерации и арифметических действиях, а также выработке вычислительных навыков.

Н е р а в е н с т в а с п е р е м е н н о й вида: х + 3 < 7 , 10 — я > 5 , х-4>12, 72:х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а «окошечком» (квадратом), например: П>0, 6+4>Ш, 7 + D < 1 0 и т. д. Учащимся предлагается подобрать такое число, чтобы получить верную запись. При выполнении таких упражнений учитель должен побуждать детей к подстановке различных чисел; например, в неравенстве Ш>0 можно подставить число 1 ( 1 > 0 ), можно 2 (2>0), можно 3 ( 3 > 0 ) и т. д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10 — от 0 до 9).

Рассматривая во II классе, например, неравенство л:+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х + 3 меньше, чем 10. В каждом таком задании дается множество чисел — значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.

Термины «решить неравенство», «решение неравенства» не вводятся в начальных классах, поскольку во многих случаях ограничиваются подбором только нескольких значений переменной, при которых получается верное неравенство.

Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами, подбирают их. Такие упражнения, как правило, выполняются под руководством учителя.

Можно ознакомить детей с таким приемом подбора значений переменной в неравенстве. Пусть дано неравенство 7-k<70. Сначала устанавливают, при каком значении k данное произведение равно 70 (при k=10). Чтобы произведение было меньше, чем 70, следует множитель брать меньше, чем 10. Учащиеся выполняют подстановку чисел 9, 8 и т. д. до нуля, вычисляют и сравнивают полученные значения выражения с заданным (70) и называют ответ.

Упражнения с неравенствами закрепляют вычислительные навыки, а также помогают усвоению арифметических знаний. Например, подставляя различные числовые значения компонентов, дети накапливают наблюдения об изменении результатов действий в зависимости от изменения одного из компонентов. Здесь уточняются знания детей о конкретном смысле каждого действия (так, подставляя значения вычитаемого, дети убеждаются в том, что вычитаемое не больше уменьшаемого и т. п.). Подбирая значения буквы в неравенствах и равенствах вида: 5 + х = 5 , 5—х=5; 10-х=10, 10-л:<10, учащиеся закрепляют знания особых случаев вычислений. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе.