Теорема. Каждый вектор x можно представить единственным образом в виде лин.комбинации векторов базиса

Пусть (1) — базис n-мерного лин. пр-ва V, т.е. совокупность линейно независимых векторов. Совокупность векторов будет лин. зависимой, т.к. их n + 1.

Т.е. существуют числа , не все равные нулю одновременно, что причѐм (иначе (1) линейно зависимы).

Тогда где разложение вектора x по базису(1) .

Это выражение единственно, т.к. если существует другое выражение (**)

вычитая из (*) равенство (**),

получим

Т.к. 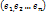линейно независимы, то . Чтд

№3

Теорема. Если - лин. независимые векторы пространства V и каждый вектор x из V может быть представлен через , то эти векторы образуют базис V

Док-во: (1)-лин.независима =>остается док-ть, что для лин.зависимы. По усл. Каждый вектор а выражается через (1): ,
рассмотрим , rang≤n => среди столбцов не больше nлинейно независимы, но m > n=> m столбцов линейно зависимы=> s=1, n

Т.е.векторы лин.зависимы

Т.о пространство V n-мерно и (1) его базис

№4Опр.Подмножество L лин. пр-ва V называется лин. подпр. этого пространства если относительно заданных в V операциях (+) и (*а) подпространство L является линейным пространством

Теорема Множество L векторов пространства V является лин. подпространством этого пространстваó выполняются

(дост) пусть (1) и (2) выполнены, для того что L подпрост.V остается доказать что выполнены все аксиомы лин. пр-ва.

(-x): -x+x=0 д. а(х + у)= ах + ау;

(а-б) и (д-з) вытекает из справедливости для V докажем (в)

(необходимость) Пусть L является лин. подпространством этого пространства, тогда (1) и (2) выполняются в силу определения лин. пр-ва

Опр.Совокупность всевозможных лин. комбинаций некоторых элементов (x_j) лин. пр-ва называется линейной оболочкой

Теорема произвольное множество всех лин. комбинаций векторов V с действ. коэф является лин. подпр V (линейная оболочка данной системы векторов лин. пр. является лин.подпр этого пр.)