Теорема Гамильтона-Кели: Каждая матрица является корнем своего характеристического многочлена

(В лекциях без док-в., если f-характ. многочлен, то f(А)=0)

№40

Опр. Собственным вектором 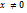оператора будем называть такой вектор, для которого выполняется равенство 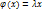, называется собственным значением, соответ. собственному вектору x оператора и P(C).

Св-ва собств. вект1) Каждому собств. вектору x соответствует (!) собственное значение .

[ctv: ]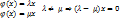

2) Если x – собст. вектор оператора то вектор , где 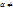0, тоже является собст. вект. для собств. зн. ( ]

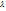Т. Если – различные собств. значения, то соответствующие им собств. вект. – образуют лин.независ. систему.

(ctv) Пусть 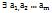не все=0 пусть для определенности . Подействуем преобр.f на обе части(1): (2); ;

(2)-(3) = 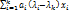=0 (*)

Лин. комб. содержит лишь (k-1) векторов. Действуем на (*) преобр. f, затем умножаем (*) на , затем из первого результата вычитаем второй => уничтожится еще один вектор, продолжая данную процедуру, придем к равенству: 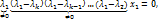но тогда 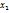= 0, но 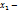собственный вектор=> против.

№41