Теорема. Ранг лин. преобр. равен рангу матрицы этого преобр. в любом базисе

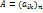матрица преобразования в данном базисе

(1), является лин. комбинацией векторов (1), но тогда каждый вектор подпространства f(v) является лин.комбинацией векторов системы ( ) (*)

в силу равенства , rang(*)=rang(A)

Т.о. ранг преобр.f равен рангу матрицы А

№34

Теорема связь между координатами вектора и его образаПусть f-лин.пр. в некотором фиксированном базисе 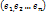пусть - произвольный вектор из V =

т.к. = A

№35

Теорема. Чтобы преобразование было взаимно-однозначным необходимо и достаточно, чтобы оно было невырожденным

Невырожденная матрица f Ax=0, имеет только одно решение x=0=> Kern f={0}

Из Kern f={0}=> Ax=0 имеет только одно решение => A-невырожденная

№36

Опр.Оператор В называется обратным оператору А и обозначается А ^-1, если АВ = ВА = E

Если А обратный для В, то А и В называются взаимообратными