
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сумма двух подпространств L является снова подпространством L
1) Пусть y1+y2  (L1+L2) <=> y1=x1+x2, y2=x’1+x’2, где (x1,x’1)
(L1+L2) <=> y1=x1+x2, y2=x’1+x’2, где (x1,x’1) 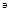 L1, (x2,x’2)
L1, (x2,x’2) 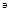 L2. y1+y2=(x1+x2)+(x’1+x’2)=(x1+x’1)+(x2+x’2), где (x1+x’1)
L2. y1+y2=(x1+x2)+(x’1+x’2)=(x1+x’1)+(x2+x’2), где (x1+x’1)  L1, (x2+x’2)
L1, (x2+x’2)  L2 => первое условие линейного подпространства выполняется.
L2 => первое условие линейного подпространства выполняется.
ay1=ax1+ax2, где (aх1) 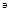 L1, (aх2)
L1, (aх2) 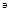 L2=> т.к. (y1+y2)
L2=> т.к. (y1+y2) 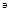 (L1+L2), (ly1)
(L1+L2), (ly1) 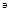 (L1+L2) => условия выполняются => L1+L2 – линейное подпространство.
(L1+L2) => условия выполняются => L1+L2 – линейное подпространство.
Пересечение двух подпр. L1 и L2 лин. пр-ва L также является подпр. этого пространства.
Рассмотрим два произвольных вектора x,y, принадлежащих пересечению подпространств, и два произвольных числа a,b: 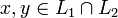 .
.
По опр. пересечения множеств: 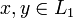

=> по определению подпространства линейного пространства: 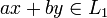 ,
, 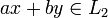 .
.
Т. К. вектор ax + by принадлежит и множеству L1, и множеству L2, то он принадлежит, по определению, и пересечению этих множеств. Таким образом:
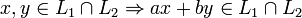 .
.
№6
Опр.Говорят, что V является прямой суммой своих подпр.  если
если 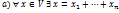 и
и 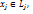 б) это разложение единственно
б) это разложение единственно
б')  Покажем, что б) равносильно б’)
Покажем, что б) равносильно б’)

При б) верно б’) 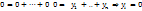
Дата добавления: 2015-04-21; просмотров: 182; Мы поможем в написании вашей работы!; Нарушение авторских прав |