Теор. Для того, чтобы оператор был СС необ. и дост., чтобы его матрица в ортонорм. базисе была симметрична

Дост. Пусть А-симм. мат, т.е. . Матрица А соотв.некоторому преобр. f, но тогда соответствует f*. Т.к. f=f*, т.е. f-cc преоб.

Необх. f-cc (f=f*) и его матр.в некотором ортн. базисе, но тогда матрицей f* является (по теореме о матрицах сопряж. операторов). , а это возможно, когда А-симм.

Теорема. Характеристический многочлен с.с.о.f в n-мерн.евкл.пр-ве имеет n действ.корней, среди кот. могут быть одинаковые

(ctv)хар.многчлн имеет компл.корень , при док-ве т.о инвар.прост-вах было установлено, что

, f(y)= (*) и L(x, y)-инв.пр-во с размерностью =z. Из (*)=> 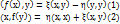левые части равны, вычитая (1)-(2) получим:

0= (т.к. ) => =0 –противоречие

№47

Теорема. Если f-сс, то собст.век-ры, отвечающие различным собств.значениям этого преобразования

Пусть различ. собст.зн. СС преобр. f. соотв. собст.век-ры, тогда ;

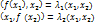лев.части равны т.к.f-cc.преоб

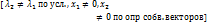
№48

Опр. Ортог.дополнением подпр.V_k называется множество всех в-ров из V_n, ортогональных каждому вектору из V_k