Теорема(Критерий подобия квадратных матриц) Две квадратные матрицы подобны т.и.т.т.к., когда они являются матрицами одного и того же лин. преобр. в разных базисах

Дост. Пусть A и B — квадр. порядка n над полем P, являются матрицами одного и того же лин. преобр. пр-ва V, тогда B=C ^-1AC (*), C-матрица перехода, С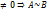

Необ. Существ. Подобные матрицы порядка n–A,B 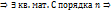выполняется (*)\

При заданном базисе между квадратичными матрицами n мерного линейного пространства существует взаимно-однозначное соответствие (по цветочку)

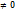Пусть f линейное преобразование пр-ва V, которое в некотором базисе имеет матрицу A, т.к C , то она служит матрицей перехода преобразования f в базисе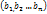

№42Алгоритм нахождения собственных значений и собственных векторов линейного оператора

Пусть базис пр-ва V. А f лин. оператор, 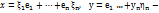собственный вектор f=> f(x)= (2)

в (1)=>перепишем (2) как )

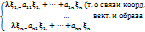ОСЛУ (**) относительно допускает 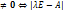=0 (*). Т.е. нужно решить многочлен n-степени, относительно 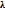(характеристич. многочл. преобр. f) => собств. значения обязательно должны быть корнями характерист. уравнения, =>для отыскания необходимо решить(*)

Пусть -корень этого ур. Подставим его в (**) и решим систему относительно , тем самым найдем координаты собственного вектора

Аналогично отыскиваются собственные векторы отвечающие другим собственным значениям

Легко видеть, что множество всех собственных векторов с собственным значением 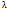совпадает с множеством всех 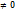решений ОСЛУ

№43

Опр. Пусть f лин.опер. n-мерного лин пр-ва V над полем P. Подпространство V’ называется инвариантным относительно f, если для 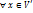образ 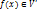. Иначе 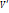инвариантно относительно f если .

Теорема. В действительном n-мерном пр-ве V всякий лин.оператор f имеет по крайней мере одно одномерное или двумерное инвариантное пространство

Пусть - какой-нибудь базис в пр-ве V и пусть 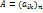- матр. оператора f в этом базисе, тогда 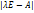многочлен n степени с вещ. коэф. Существует 2 возможных случая: хар. многочлен имеет корень

1) 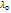-вещественный. Тогда система для нахождения собст.вектора (*) имеет ненулевое решение, кот.опред. собстве вектор отвеч.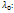

. Очевидно, одномерное подпр. L( 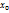)-инварант. подпр. относительно f

2) = 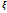+ i-компл. Подставим корень в сист. (*) получим, что она имеет 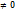решение: (‘) Подставляя (‘) в (*), перенесем члены с 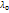в правую часть получим

Отделяя вещ и мним. части перейдем к след.сист. (*) и (**)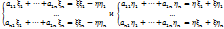

Введем в рассмотрение векторы 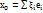и

Ясно, что x,y 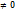(собст.векторы). тогда в (*)и (**) примут вид 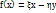, f(y)= (***),=> подпространство порожденное векторами x и y (L(x,y)) инвариантное подпр. oператора f(x)

Действительно, пусть 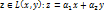, f(z)= 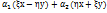= y=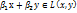

Размерность 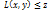. Подпр. 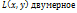, т.к. если бы 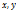были лин.завис. y=kx, то f(x) 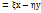= 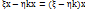и x был бы собственным вектором преобр с вещ.собств. значением , что невозможно

Следствие: пусть f-лин.оператор вещ. лин. пр-ва Vразмерности (zn+1), где n-натур.,тогда существует хотя бы одно одномерное инвариантное подпр. f, т.к. у f хотя бы один собств.вектор, отвечающий вещ.собст.значению—корню многочлена 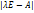нечетной степени

№44

Теперь будем считать, что V- евкл.пр-во (т.е. в Vопред. операция скалярного умножения)

Опр. Лин.операторы f и называются сопряженными если имеет место равенство 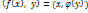. Очевидно 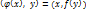. (1)

Теорема. Пусть f и сопряженные операторы в V, ортонорм. базис вV. А—мат. f, а В — мат в (2). Тогда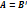

Запишем (1) для пары векторов :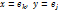

( f ( ),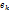

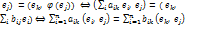
s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="14"/><w:sz-cs w:val="12"/><w:lang w:val="EN-US"/></w:rPr><m:t>.</m:t></m:r></m:lim></m:limLow></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> ( )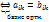

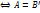
№45