Теорема. Для всякого сс преобр. найдется хотя бы один ортонорм. базис, состоящий из собст. векторов этого преобр., в кот. матрица преобр. имеет диагональный вид.

Согласно теореме (*)/*Характеристический многочлен с.с.о.f в n-мерн.евкл.пр-ве имеет n действ.корней, среди кот. Могут быть одинаковые*/у с.с.о.f есть дейст.собст.значение x₀, ему отвечает собст.вектор e₁, длину кот.,не нарушая общности можно считать=1.

Пусть Р-совокупность всех векторов P и R имеем , т.е. P P подпр. V являющееся доп. к L( ). По лемме[Ортогон. доп. k-мерного подпр. V_k есть (n-k)-мерное подпр.] dimP=n-1. Покажем что P-инвариантное подпр.оператора f

По теореме(*) имеется хотя бы одно вещ.собст.знач. опер-ра f, кот. отвечает соб.вектор P

Продолжая это построение получим n собст.векторов образ.ортон.базис, т.к. f )= обст. зн. f, то матр f в базисе имеет вид

A=
№50

Если - корень кратности m характерист. многочлена самосопряженного преобразования f, то ему соответствуют n-(n-m)=m линейного независимых систем векторов.

Согласно теореме /*для всякого сс преобр. найдется хотя бы один ортонорм. базис, состоящий из собст. векторов этого преобр., в кот. матрица преобр. имеет диагональный вид.*/

базис в кот. матрица преобразования имеет диагональный вид. В этом же базисе

E-A= (*)

Пусть, например корень кратности m характерист.многочлена, т.е. , , тогда в матрице обращаются в 0 m строк, при 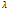, а остальные диагональные элементы не равны 0

система = имеет лин.независимых решений собственных векторов, соответствующих собственному значению

1. Опр. лин. пр-ва. След.из аксиом лин. пр-ва. Док.одно

2. Размерность и базис лин. пр-ва. Док., что любой вектор лин. пр-ва можно (!) образом разложить по базису.

3. Док, что если система векторов лин незав. и каждый вектор лин. пр-ва может быть разложен по векторам этой системы, то указанная система векторов является базисом.

4. Необ. и дост. усл. для того, чтобы некоторое подмножество векторов лин пр-ва было лин. подпр. Док, лин обол данной системы векторов лин пр-ва является лин.подпр. этого пр-ва.

5. Док сумма и пересечение двух подпр лин прос являются лин подпр этого пр-ва.

6. Док, что слагаемые подп прямой суммы пересекаются лишь по 0. Док обратное. Необ и дост усл чтобы лин. пр-во являлось прям сум своих подпр. Размерность прямсуммы.

7. Док, что любая квадр невырож мат - матр перех от одного базиса к другому.

8. Т о связи между координ вект в разных базисах.

9. Основная теорема о линейной зависимости.

10. Док, что все макс линейно независимые системы векторов содержат одинаковое количество векторов.

11. Экв системы векторов. Т о == рангов экв систем.

12. Теорема о ранге произведения матриц.

13. Теорема об изоморфизме лин пр-в. Значение теоремы.

14. Док, что мн-во решений ОСЛУ с n, являются лин. подпр пр-ва P^n. Т о размер этого подпр. Т о связи между реш неоднородных и соответствующих однородных систем.

15. Евк пространство. След аксиом скал произв, н-во К-Буняк, н-во , об. т. Пифагора.

16. Док, что любая сист. попарно вект, 0, лин. незав..

17. Т о ортон базиса. Процесс ортогонализации.

18. Т о представлении скал. произв в координ форме.

19. Теорема об изоморфизме евклидовых пространств.

20. Унит пр-во След аксиом скал произв, н-во К-Буняк, н-во , Ортон базисы, скалярное произведение в координатах.

21. Необ. и дост. усл. симм. (кососим.) билин. формы. Представление билин. формы в виде суммы симм. и косос

22. Преобразование мат билин формы при переходе в лин пр-ве к новому базису. Ранг билинейной формы.

23. Квадре формы. Ранг квадр формы. Т о базиса, в кот квадр форма имеет канонвид. Метод Лагранжа

24. Метод Якоби приведения квадр формы к канон

25. Кв. формы в вещ лин пр-ве. Закон инерц кв форНеоб признк «+» определ квадр формы. Кр Сильвестра. Следс.

26. Необ и дост условия + полуопределен кв.формы.

27. Необ и дост усл - определ кв формы (след из кр Силь).

28. Теорема о «--» полуопределенности кв формы.

29. Опред Грама. Т об определит Г. Обоб н-ва К-Буняк.

30. Лин преобр (операторы) лин пр-ва. Св-тва

31. Док, что если f и g — лин преоб пр P, то f+g, fg, lg — лин преоб. Полином от линейного преобразования.

32. Матр лин преобр. Т о матрице f+g, fg лин преоб

33. Ранг и ядро лин преобр. Докчто ранг лин преобр == рангу матрицы этого преобразования в любом базисе.

34. Т о связи коорд вект и образа при лин преоб лин пр-ва.

35. Док, невыр преобр -- необ и дост усл его взаим однозн

36. Необ и дост усл обратимос лин опер. (!) обратн опер.

37. Т о завис между матр преобр в разных базисах.

38. Док одно из свойств подобных квадр матриц.

39. Т о == характерист многочленов мат. Т Гамил-Кэли.

40. Соб зн и собсте век лин преобр. Т о лин незав собст вект., отвечающих различным собственным значениям.

41. Критерий подобия квадратных матриц.

42. Алгоритм нахождения собс век и собст зн лин операт

43. Инвариантные подпр. Теорема об инвар подпр

44. Сопр. операт. Док, что матрицы сопряж опер, в ортонм базисе, то A = B^т.

45. Док, в кон.мер. евк пр-ве кажд лин оп имеет (!) сопр.

46. Необх и досте усл самосопр преоб. Т о корнях характ многочл сс преобр в n-мерном евк пр-ве.

47. Док, в сс преоб собс вект, отвеч разным собст зн пр .

48. Ортог доп подпр. Док, что орт доп k-мерн подпр V^k есть (n-k)-мерное подпр

49. Док, для cc преобр найдется хоть1 ортон базис, сост из собс вект этого преобр, в кот мат пр имеет диагон вид

50. Док, что если l - корень кратн m хар многочл сс преобр f, то ему соответс n-(n-m)=m лин незав систем вект

51. Построение ортон базиса, сост из собст вект сс преоб

52. Орт преоб. Док, что орт преобр переводит ортон базис в ортон базис. Док, лин преоб, переводящее хоть 1 ортон базис в ортон ортогонально.